The Triad of Systems: Input, Process, Output

For a long time, I stumbled upon déjà-vu - a triad that appears everywhere, from the design of computers to the way we think about behavior and algorithms.

🥚	🔆	🐣
🟥	🔴	🔺
1️⃣	2️⃣	3️⃣
💛	💚	💖

It’s so universal that it feels like a law of nature: Input, Process, Output.

However, my brain does not do a good job of recording experience regarding such pattern. Sometimes they’re subtle, hiding in the details of seemingly unrelated fields. Other times, they’re so obvious that you wonder how you didn’t see them before.

That’s the reason I start writing this post, solidify the déjà-vu hopefully into a pattern just like the purpose of the book Design Patterns - Elements of Reusable Object-Oriented Software collecting similar design experience in software framework.

Von Neumann Architecture

I believe this is where the skeleton of the triad first took root in my mind.

The von Neumann architecture, the backbone of modern computing, is built on this triad. You have

input devices (like keyboards or sensors),
a processing unit (the CPU), and
output devices (like screens or printers).

+-------------------+       +-------------------+       +-------------------+
|                   |       |                   |       |                   |
|    Input Device   | ----> |    Central        | ----> |    Output Device  |
|   (Keyboard,      |       |    Processing     |       |   (Monitor,       |
|    Sensor, etc.)  |       |    Unit (CPU)     |       |    Printer, etc.) |
|                   |       |                   |       |                   |
+-------------------+       +-------------------+       +-------------------+
                                ^       |
                                |       |
                                |       v
                        +-------------------+
                        |                   |
                        |    Memory Unit    |
                        |   (RAM, Storage)  |
                        |                   |
                        +-------------------+

Whether or not I had encountered this input-process-output sequence before, my first “ah-ha” moment came while reading the book Introduction to Computing Systems: From Bits & Gates to C/C++ & Beyond > Chapter 4.

To this day, I remain deeply impressed by von Neumann’s discovery, truly remarkable. It also enforces my belief in the value of interdisciplinary thinker, much like von Neumann, a mathematician working in a broad interdisciplinary perspective.

Computational Science

Alan Edelman , professor in applied mathematics of MIT, has a very interesting view on the distinction between computer science vs. computational science. In his view, the computational science adds an extra layer with physical world where computer science operates in a more abstract realm.

+---------------------------------------+
|                                       |
|    data ⟶ input ⟶                     |
|          process ⟶ model ⟶            |
|              visualize ⟶ output       |
|                                       |
+---------------------------------------+

The computational science can be summed up by a simplified workflow like the preceding diagram. To connect with physical world,

data: this is the light shining from the physical world
visualize: this is our impression on the physical world

Let’s get Prof. Edelman’s dog Philip involved.

Input The following portrait of Philip is the input, a digital image with RGB info describing Philip.

Process We want to ask, “what color remains in our mind after closing our eyes thinking of Philip”? To answer this, we can simply take the mean of the RBG🟥🟩🟦 values of this image.

function mean_color(image)
	r = mean(get_reds(image))
	g = mean(get_greens(image))
	b = mean(get_blues(image))
	return RGB(r, g, b)
end
mean_color(philip)

Output The output is

Oh, I see, well.. This is more or less Philip… as he is a Corgi.

Computational Design

7 years ago, when I first read Rajaa Issa’s book Essential Algorithms and Data Structures for Computational Design in Grasshopper, I learned that every algorithm has 3 building blocks: input, process, and output.

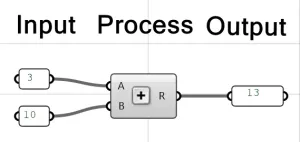
This triad can be as complex as many components tied together, and can also as simple as an “Add” component.

This insight blows up my mind. Back in 2018, I didn’t see the pattern of this triad while my Grasshopper canvas was often a tangled mess of wires connecting components

This is a powerful insight shift. Every time I need to deliver either a Brep or a landscape contour line, or any other output, the ultimate goal become figuring out the connection from input to output.

It’s no wonder, then, a Grasshopper component typically has connectors on 2 sides .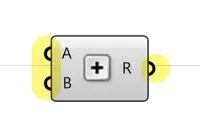

Once the input and output are set up, we can simply focus on the process. Often, this involves breaking the process down into a smaller, more manageable steps.

Identify the Need in Product Creation

Next, I want to explore a field seemingly unrelated to computation. When Xiaolai discusses how to fulfill people’s need in product creation in his book, he outlines 3 steps:

purpose: the goal is to avoid creating a product that no one will use.
method: one approach is to start by solving your own problems or needs.
outcome: at the very least, you will have one customer - yourself.

If we skim this 3 steps, we indeed realize the purpose. Mathematically speaking, avoid no one use your product means ensuring that there exists one person using your product.

\exists(\text{1 person}) \implies \text{avoid no one}

In practice, we can also see how the method influences the outcome. This is essentially the same principle as in computational science. We adjust our model to achieve a better result.